In the context of this exercise, lets suppose having the two dependent following function:
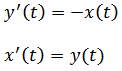
With initial conditions
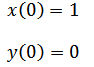
The equation of a circle look like the following
![]()
where the r is a constant.
If we add our equations at 0, the following will be true
![]()
We are now going to be using Euler methods and the Runge-Kutta to model a circle of a radius 1 using the above mentioned equations.
Forward Euler method
Based on the equations
![]()
We can write the following based on our example.
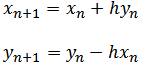
Here is the Matlab code deriving from the above.
clc; clear all; h=0.2; % value of the step, you can vary this to see how it affect the graph N=51; x=zeros(1,N); y=zeros(1,N); x(1)=1; %initial value x(0) y(1)=0; %initial value y(0) %iteration with 50 step % Forward Euler method for i=1:N x(i+1)=x(i)+h*(y(i)); y(i+1)=y(i)-h*(x(i)); end angle=linspace(0,2*pi); % used to plot the unit circle plot(x,y,'r',sin(angle),cos(angle),'b')
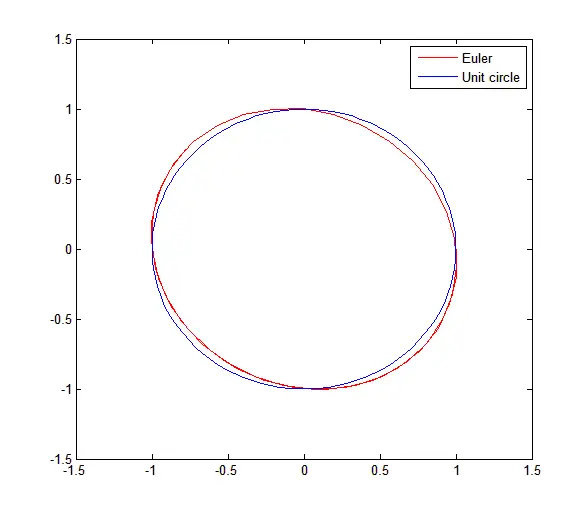
And the following plot results from it.
Backward Euler method
Just like the previous method we will start from the formula, then the derivation according to this exercises, the Matlab code and then the graph
Formula
![]()
Derivation
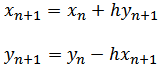
we need to arrange the above equation for it to look like the following (substituting and putting n+1 elements on one side and n elements on the other side )
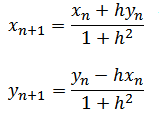
Matlab code
clc;
clear all;
h=0.2;
N=51;
x=zeros(1,N);
y=zeros(1,N);
x(1)=1; %initial value x(0)
y(1)=0; %initial value y(0)
%iteration with 50 step
% Forward Euler method
for i=1:N
x(i+1)=(x(i)+h*(y(i)))/(1+h^2);
y(i+1)=(y(i)-h*(x(i)))/(1+h^2);
end
angle=linspace(0,2*pi); % used to plot the unit circle
plot(x,y,'r',sin(angle),cos(angle),'b')
legend('Euler', 'Unit circle')Plot
Semi-implicit Euler method
Derivation
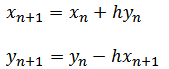
Matlab code
clc;
clear all;
h=0.2;
N=51;
x=zeros(1,N);
y=zeros(1,N);
x(1)=1; %initial value x(0)
y(1)=0; %initial value y(0)
%iteration with 50 step
% Forward Euler method
for i=1:N
x(i+1)=x(i)+h*(y(i));
y(i+1)=y(i)-h*(x(i+1));
end
angle=linspace(0,2*pi); % used to plot the unit circle
plot(x,y,'r',sin(angle),cos(angle),'b')
legend('Euler', 'Unit circle')Plot
Runge Kutta method
Derivation
Working the same way with y
Matlab code
clc;
clear all;
h=0.2;
N=51;
x=zeros(1,N);
y=zeros(1,N);
x(1)=1; %initial value x(0)
y(1)=0; %initial value y(0)
%iteration with 50 step
% Forward Euler method
for i=1:N
xk1=y(i);
yk1=-x(i);
xk2=y(i)+0.5*h*yk1;
yk2=-(x(i)+0.5*h*xk1);
x(i+1)=x(i)+h*xk2;
y(i+1)=y(i)+h*yk2;
end
angle=linspace(0,2*pi); % used to plot the unit circle
plot(x,y,'r',sin(angle),cos(angle),'b')
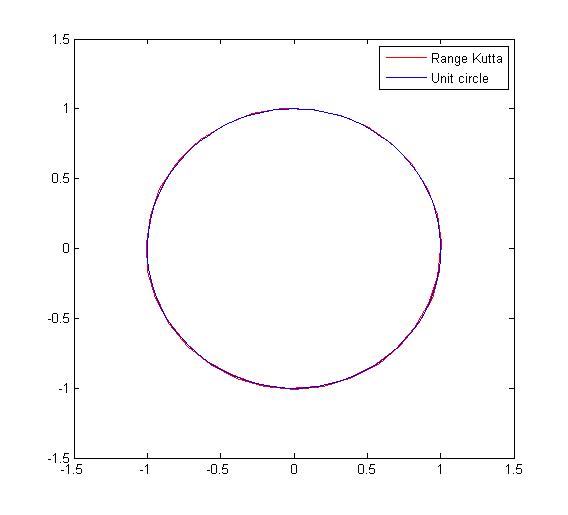
legend('Range Kutta', 'Unit circle')Plot



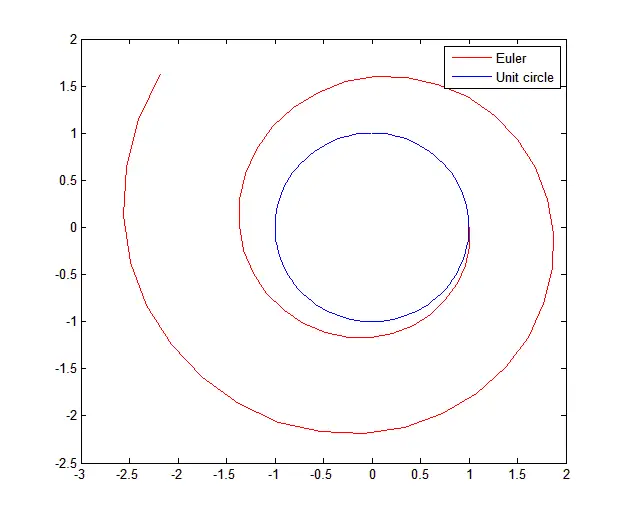
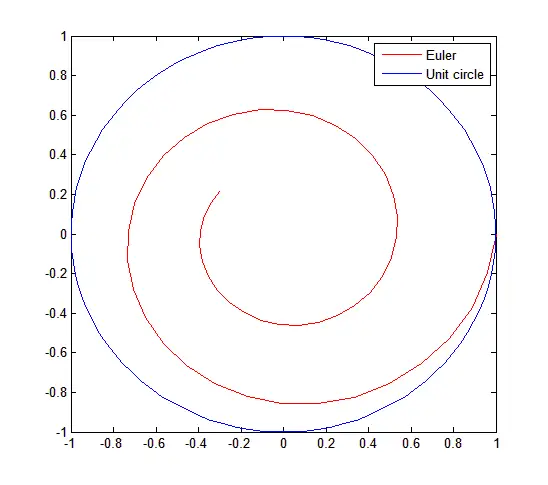
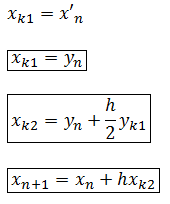
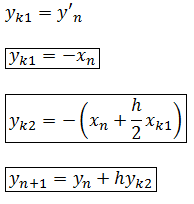
Comments
One response to “Euler VS Runge kutta – Circle – Matlab code”
Can you please explain how you arrived at the various equations for the Runge-Kutta method?